graph bundling

3DHEB is an algorithm that bundles edges of a graph to reveal connectivity patterns. It allows to tackle large graphs and specify bundling criteria to cluster edges (in addition to the default criteria based on  proximity).

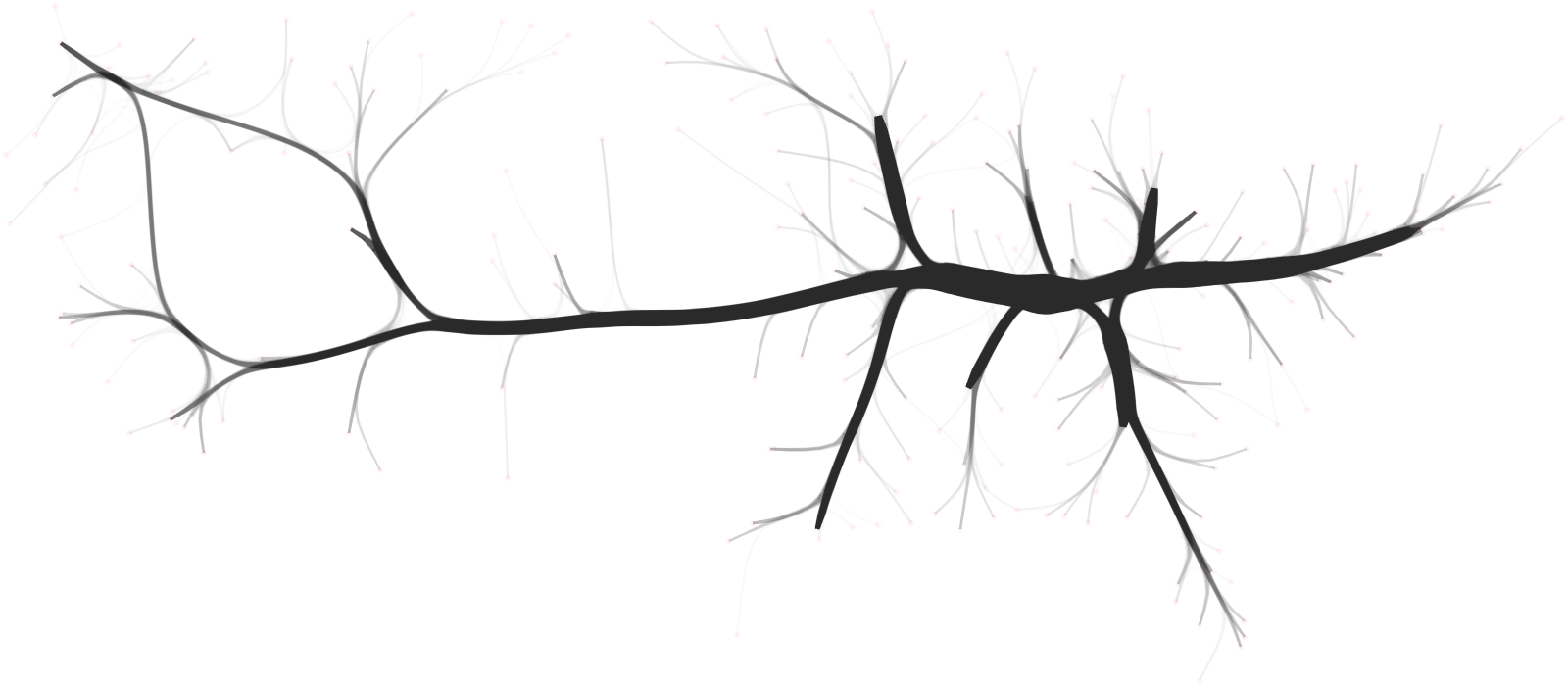
In the above image, the nodes of the graph are airports and the edges (aka arcs or links) of the graph are trips between airports, with weight equal to the number of trips between the origin-destination airports. Edges are bundled iteratively based on their spatial density, revealing connectivity patterns.

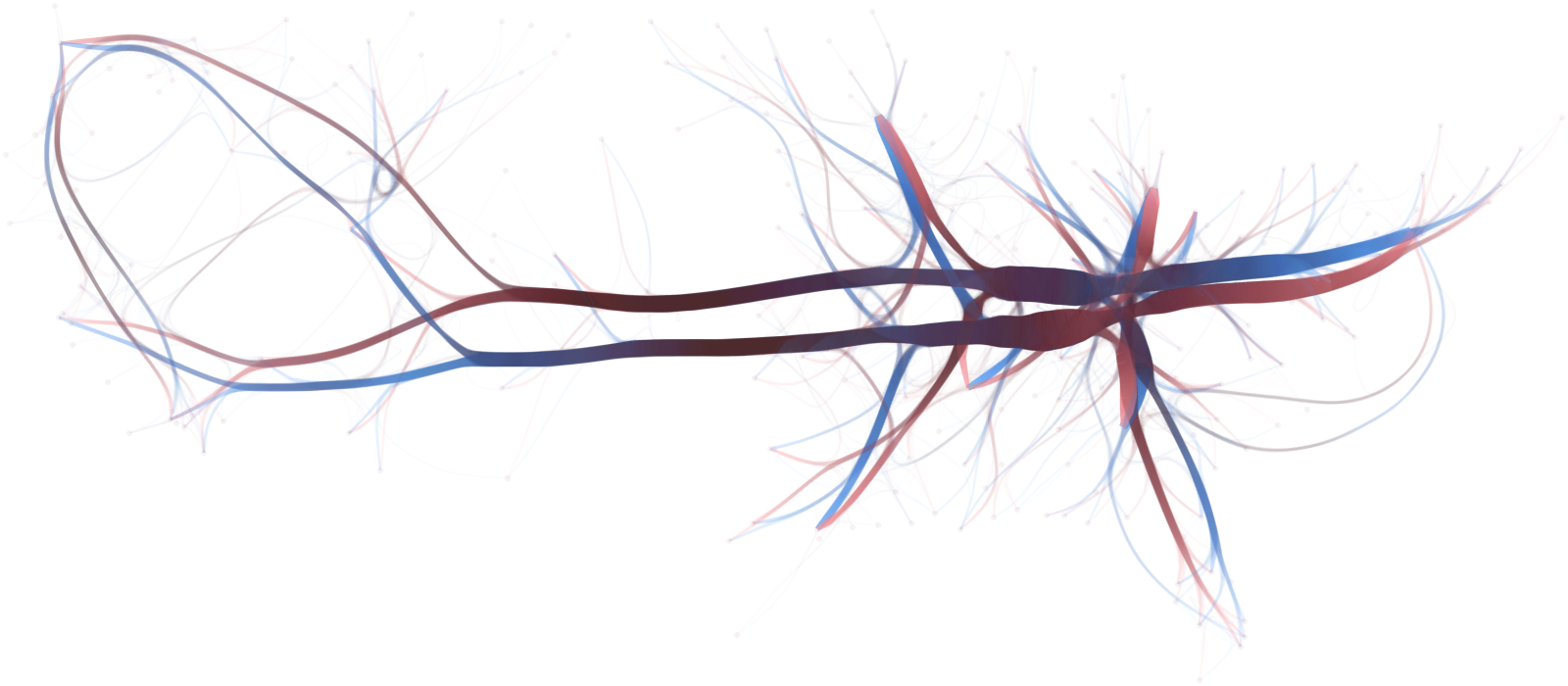
By adding bundling criteria the algorithm can reveal more patterns. In the above case, the direction of the flow is taken into account to produce different density maps that interact among them. Flows that have opposite directions are repealed while flows that have similar direction are attracted. Gradient colouring allow for a better understanding of the direction of the flows, with edges being blue at the origin and red at the destination, passing through black.

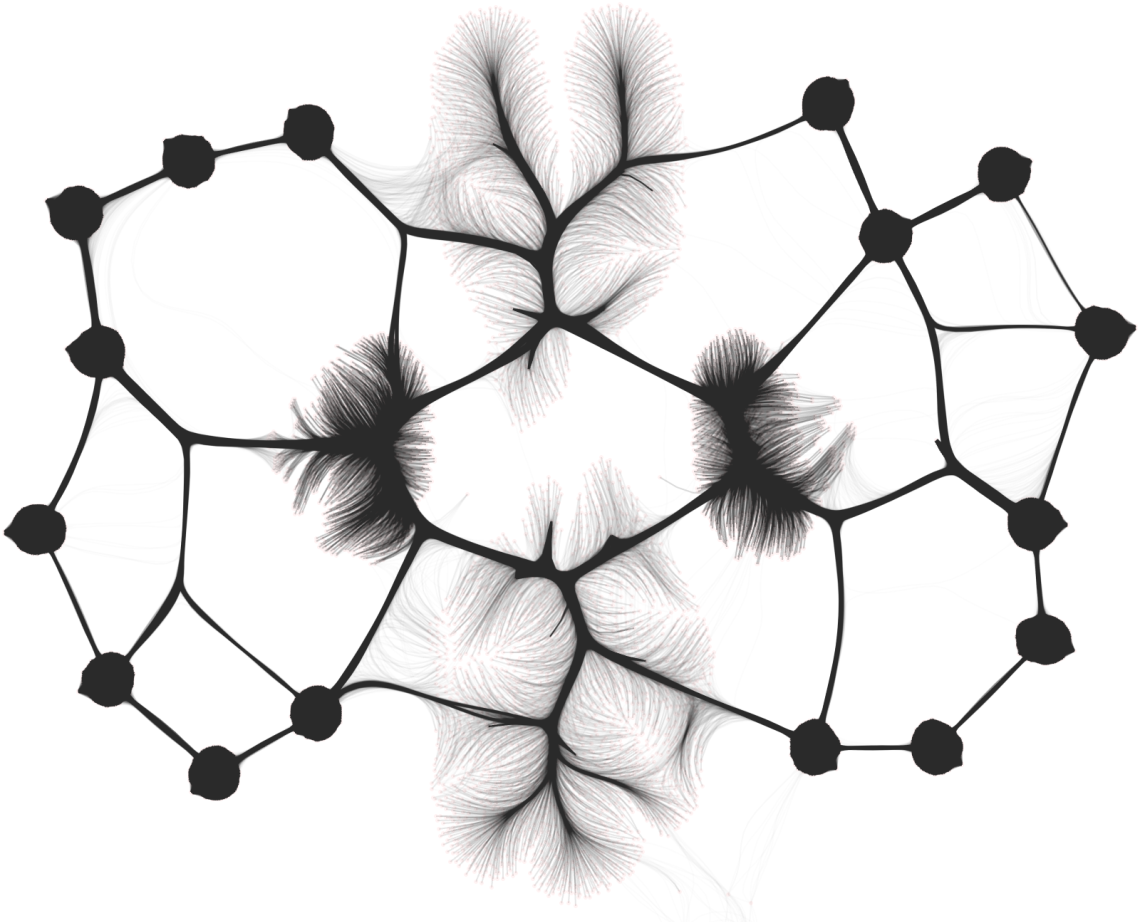
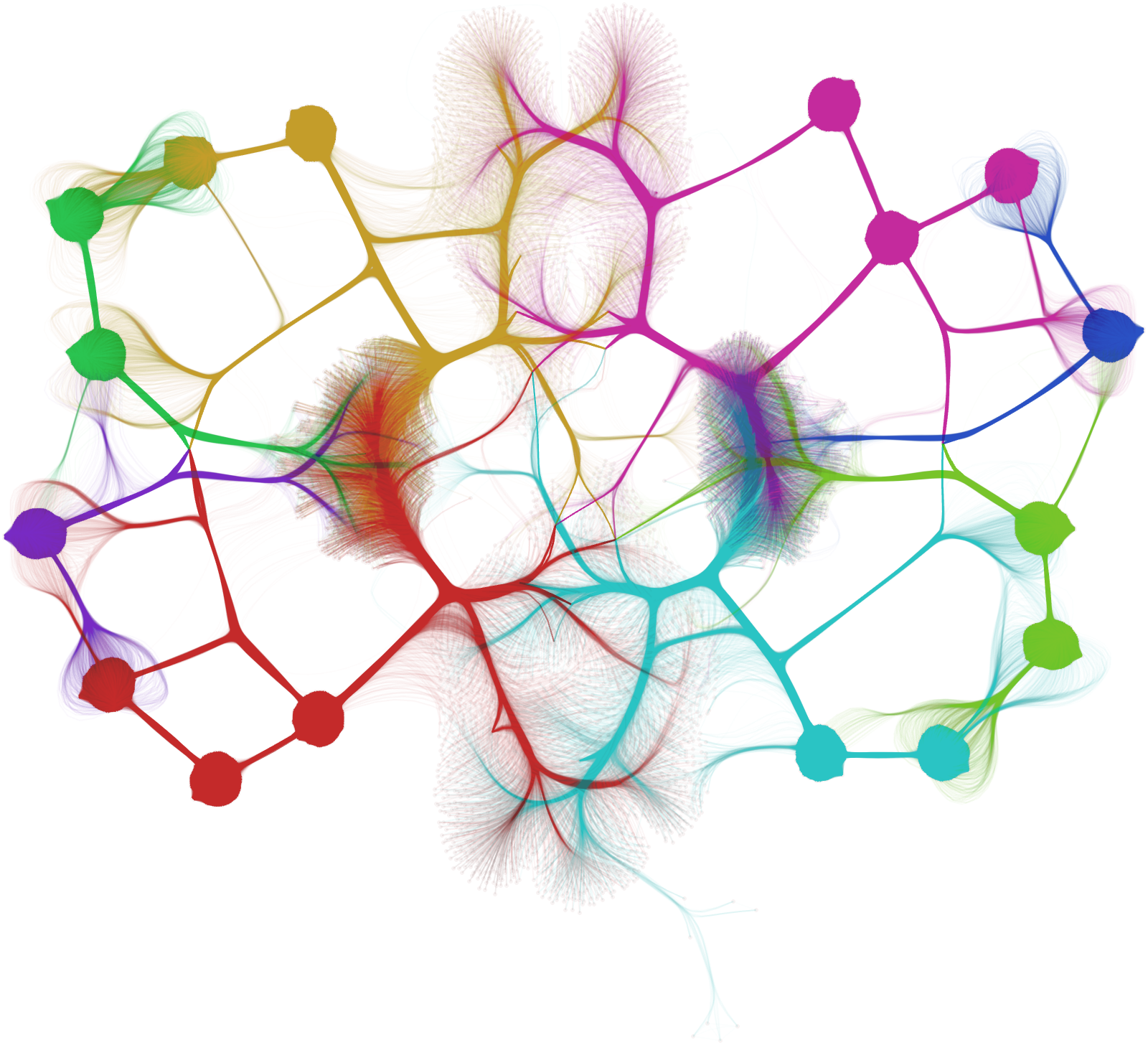
The algorithm can tackle large graphs like the one above with 5 million edges. Bellow, edges are clustered into 8 clusters taking into account their origin and destination, with each cluster being represented by different color.

I have created an online tool where you can have a go and play with the different parameters of the algorithm. The code is available at github and more details can be found in the paper 3D Density Histograms for Criteria-driven Edge Bundling.